Quo Vadis - International Conference
FIG Working Week 2000, 21-26 May, Prague

Proceedings

Key words: Israel geoid, Stokes, gravity anomalies. 

This paper presents the final results of a pilot-project, for mapping an accurate geoid of the State of Israel. The purpose of the project was to develop a feasible methodology, assemble all necessary data, design and test field procedures and finally to work out a suitable analysis algorithm, including the respective computer programs. The project was funded and supported by the Survey of Israel over a period of five years between 1994 and 1999. An area of about 600-sq. km on and around the Carmel Mountains served as a field laboratory and proving ground. The ultimate goal was to render a geoid map of the pilot area with a one-sigma accuracy of 4 cm. The geoid map was compiled from three independent data sources that complement each other:

• Measured geoid undulations (indirectly - by GPS and trigonometric leveling) at a network of control points. The network density was set intentionally high by a factor of three to four in order to provide means for testing the quality of the map.

• A global gravity model of the highest order available. Over the years 1994-1999 a number of gravity models were used, beginning with OSU'91, followed by EGM'96 and finally - the 1800-order GPM'98B model.

• A dense grid of free-air gravity anomalies (3') extending up to a distance of 2^o from the pilot area. Within the state boundaries we used directly measured anomalies. At sea and beyond the state boundaries we depended on free-air gravity anomalies, reconstructed from a dense Bouguer anomalies grid and a corresponding DTM of land-surface and sea-floor topography.

The computational procedure based on the Remove & Restore approach is as follows:

• Transform the free-air-anomalies grid into a grid of residual anomalies, by removing respective model (GPM'98B) anomalies.

• At every control point, compute model geoid undulations (including a number of corrections such as "zero order" undulation, the effect of global elevation, indirect effect) and add Stokes integration of the residual free air anomalies field.

• Subtract from the above (b) "crude prediction" the "measured" undulations and create a control-point correction field. Interpolate the correction field into a contour map or a grid. At any point within the grid boundaries, geoid undulation can be predicted now by subtracting the interpolated correction grid value from the "GPM'98B plus Stokes" crude prediction.

Three factors dominate the accuracy of the final geoid map:

• Density of the anchor points.

• Over-all fit of the gravity model to the local geoid.

• Radius of Stokes integration of the residual free air anomalies field.

With anchor points spaced 5-20 km apart; employing the GPM'98B model and finally extending Stokes integration up to 2^o, we obtained an accuracy (one-sigma) of 2 cm or better. Although our accuracy estimates were based on sound analysis principles, they may seem a bit too optimistic. Analysis of additional test fields should confirm our "optimistic" results or else - define more realistic accuracy estimates.

Dr. Dan Sharni
Geodesy
Technion
32000 Haifa
ISRAEL
Tel. + 972 4 829 2482
Fax + 972 4 823 4757
E-mail: sharni@techunix.technion.ac.il

Haim B. Papo
Geodesy
Technion
32000 Haifa
ISRAEL
Fax + 972 4 823 4757
E-mail: haimp@tx.technion.ac.il

The advent of "GPS leveling" and the need for medium level accuracy and fast orthometric heights have renewed the interest in precise geoid maps. In the past five years the authors have been involved in a joint project with the Survey of Israel, designed to develop and test surveying and analysis procedures for the creation of a precise geoid for the State of Israel. The target accuracy of geoid undulation differences between neighboring points was set at 4 cm. An experimental laboratory was established in the form of a pilot-project area on the Carmel Mountains near Haifa. A dense network of some 70 control points was marked and surveyed in the pilot-project area.

The project proceeded chronologically along two distinct phases:

1. Field surveying and subsequent rigorous adjustment of two complete and independent vertical control networks (GPS and trigonometric leveling);

2. Collection of gravimetric and topographic data of the pilot area and its neighborhood up to a radius of 2^o and development of optimal strategies and a respective algorithm for modeling high-frequency variations of the geoid.

With the completion of phase (a) we had at our disposal a network of 66 control points with an estimated accuracy of undulation-differences between neighboring points of the order of 2 cm. Figure 1 shows a map of geoid undulations over the pilot-project area based on all 66 points.

Phase (b) of the project was complicated and lengthy, due to a severe lack of gravimetric data beyond the state's boundaries. We applied data from various sources and modalities - gravimmetry, DTM, bathymetry - to reconstruct and complement the incomplete gravity-anomaly field. The well-known "Remove & Restore" procedure, using a global gravity model, was then utilized. We were able to bring our project to a successful conclusion only after the introduction of a new gravity model (GPM'98B). GPM'98B was the first global model to employ gravity data from our area.

Measured undulations (actually: computed undulation-differences) were derived from GPS-height differences and short-leg trigonometric leveling measured between points of a control network. The total number of points with directly measured geoid undulations was 66, where the pilot project covered an area of some 570 square km. The average distance between control points was thus 3-4 km, a rather dense spacing. The high density of control points was intended to provide means for assessing undulation prediction quality at different control point spacings.

The observations were carried out by the Survey of Israel, as a static GPS survey with 4 or 7 receivers. Each of the 66 control-points, as well as 10 more triangulation points (5 of which were elevation benchmarks) was occupied for 2 sessions of 45 minutes each /Sharni et.al, 1998/. Adjustment of the measured GPS vectors resulted in a vertical control network with a standard deviation of the order of 12 mm (8-15). The nominal accuracy might seem optimistic but we found in the final analysis of the undulation-prediction results that it was fairly representative.

The pilot-project afforded the first opportunity, in Israel, to analyze, write specifications, field-test and execute extensive precise trigonometric leveling. The loop closures of the measured elevation differences indicated that a 3rd-degree leveling requirements (10.k^1/2, where k is the loop-length in km) can be readily met. Using 5" total-stations, limiting measuring distances to a maximum of 120 m, pointing to the center of the "coaxial" prism while it is supported on a tripod (not hand-held) etc. were all part of a long list of specifications. In /Sharni et.al., 1998/ we have reported in complete detail of our experiences and achievements with trigonometric leveling. The final adjustment of the measurements into a vertical control network (of orthometric heights) produced a-posteriori error estimates that agreed very well with our a-priori ones - indicating proper weighting of the measurements. The estimated error per km came out 5.7 mm; the accuracy of the adjusted elevation difference between points at 10-15 km distance was 15 mm; the maximum error, propagated over the entire project area (air-distance of the order of 40 km) reached only 22 mm.

The ellipsoidal (GPS) vertical network was adjusted as a free network with datum derived from the nominal heights (WGS84) of the above mentioned five benchmarks. We did not bother to investigate how well the nominal heights of those benchmarks refer to the WGS84 ellipsoid. We were reassured by their apparent consistency (height differences) with our GPS measurements. The orthometric vertical network was adjusted also as a free network. Here datum was derived from the nominal heights of some 69 points as taken from the catalogues of the first order vertical control network in Israel. Thus the datum of our geoid undulations is as a matter of fact quite arbitrary and is valid only within the limit of the pilot project. All along in our pilot project we were interested in producing precise undulation differences, which are datum-independent. Mapping the geoid over the whole State of Israel is an entirely different story and there appropriate measures will have to be taken to insure a uniform datum. Estimated accuracies of our geoid undulations were derived from the covariance matrices of the above two free vertical networks. To generalize the results for the entire network we could say that standard deviation of undulation-difference between any two neighboring control-points 10-20 km apart is of the order of 20 mm. It was comforting to know that we would have a wide margin of safety, from our goal of prediction accuracy of 40 mm - even after contributions to the error budget of representation and interpolation would be accounted for.

In our project we counted on gravimmetry to provide the means for modeling the finer details of the geoid surface. The basic modeling tools were the well-known Remove & Restore process and Stokes integration. The area in the proximity of the project is covered by observed, discrete, gravity anomalies (and thus it can be accounted for by Stokes integration). A global gravity model represents the gravimmetry of the outlying areas (beyond the limits of Stokes integration). Appropriate reductions and corrections are applied to the data and model results, for compatibility.

Initially we applied in our analyses the OSU'91A model. We knew that this model did not incorporate enough data from the Middle East, and consequently it may not be able to represent it very well (it may not conform with our measured undulations). Later on, NIMA released its EGM'96 model /Lemoine, 1998/, which contained already some skeletal gravimmetric input from Israel. We received it courtesy of Professor Richard H. Rapp, The Ohio State University. The EGM'96 model seemed to fit better with our results - though we encountered problems at sea, along the shore. Finally, Professor Wenzel's model GPM'98B was put at our disposal after we did supply him with gravity data from Israel. The 1800 order GPM'98B global gravity model seemed to fit our measured undulations remarkably well.

The Geophysical Institute (Dr. Yair Rotstein, Director) made its file of observed gravity values available to our project. It contained some 48,500 measured g values, mostly in Israel and Sinai, between latitudes 27.7^o-34.3 ^o and longitudes 32.4 ^o-36.1. We applied atmospheric reductions and through the gravity-formula-1980 of /Moritz, 1980/ we produced "observed" free-air gravity anomalies, on land. At a later date it was noticed (courtesy of the late Professor Wenzel, then at The University of Karlsruhe, Germany), that our observed gravity data had not been reduced to IGSN'71 - as required to fit GF'80. The nominal reduction for Israel was of the order of 12.5 mgal, whereas a cooperative effort between Israeli and Jordanian scientists, investigating the Dead Sea area, suggested a reduction of 15 mgal as more appropriate /Ten Brink, 1993/. This reduction (15 mgal) was applied to the observed gravity data. The point values were averaged into a regular, basic grid of 3 by 3 arc-minutes or 0.05 by 0.05 degrees (with a denser grid of 0.015 by 0.015 degrees within the project area).

The data included some obvious mistakes, as well as blank areas, where not even one observation was available to compute an average free-air anomaly for the respective cell. Those zeroes were replaced by more realistic values, before applying Stokes integration. We did this mostly by auto-correlation to neighboring cells.

Israel is a narrow state, with a mostly N/S extent. On the west is the Mediterranean Sea. We did not have access to gravity data from any of the neighboring states. The observed gravity anomalies around the project area provided coverage of no more than 0.5 degrees in the north-east-south directions (land), while to the west (sea) we had no data at all. The gravimmetric data was clearly insufficient for a reliable Stokes integration. Thus it became necessary to obtain indirect free-air anomalies, from other available sources. An important source of gravity was a dense grid of Bouguer anomalies of a wide area around the project, collected and collated by the Geophysical Institute. From this we could reconstruct free-air anomalies, utilizing available bathymetry of the East Mediterranean (initially from Dr. John Hall, Geological Institute and later on from US Naval Oceanographic Office). We needed also DTM data for free-air anomaly reconstruction on land. We used at first Dr. Hall's DTM until we obtained finally US Geological Survey (EROS) data - a dense grid of 30 by 30 arc-seconds). It was important to check the consistency between bathymetry and DTM on land. In reconstructing free-air anomalies over lakes, we took care of the unusual lake-surface elevations in Israel (-210 m for Lake Kinneret and -405 m for Dead Sea). In addition to water depths, we considered water-density (1.00 gr/cc for the Kinneret and 1.13 for the northern part of the Dead Sea; maximum water density is close to 1.4! in the south). Some smoothing was necessary, to fit reconstructed to observed anomalies, mainly along the sea shore and the state borders. Thus we were able to complete the construction of a grid of free-air anomalies extending well beyond 2^o from the borders of Israel. We regarded 2^o as a reasonable limit for Stokes integration.

Following the well known R&R process we employed the global gravity model GPM'98B to evaluate two free-air anomalies grids corresponding exactly to our two grids of 0.05^o and 0.015^o cell size. The grids of model anomalies were subtracted (removed) from the respective average (or reconstructed) grids thus producing two grids of residual anomalies. The same model (GPM'98B) was used to evaluate height anomalies (a first step towards the restoration of undulations) at each of the 66 control points. We completed the computation of model geoid undulations by applying a number of corrections to the height anomaly and by adding the Stokes integral. The corrections were for "zero-order" undulation, for the effect of global elevations and for the indirect effect of the topography. At each control point we added the result of Stokes integration of the residual free-air anomalies field. The final result for each control point was regarded as a "crude prediction" of its geoid undulation.

Two limits were defined for Stokes integration with respect to any computation-point: the inner-limit related to the specific grid cell within which the computation point is located, and the outer-limit, beyond which integration is terminated. Stokes integration between the computation-point and the inner-limit was replaced by evaluation of the effect of a spherical cap. Several tests were carried out to determine the optimal size of the inner-limit and it was set finally at 0.44 of the finer grid size (0.015^o). The outer limit was set at 2^o, as mentioned above. The residual free air gravily anomalies for the project were arranged in a basic grid of 0.05^o, between latitudes 30.0^o-35.5^oand longitudes 32.0^o-38.0^o. The finer grid 0.015^o, was reserved for the pilot area, between latitudes 32.4^o-33.0^o and longitudes 34.7^o-35.3^o. Thus the total result of Stokes integration at any point within the project area was the sum of three integrals representing the spherical cap, the denser grid and the basic grid.

The height-anomaly differs slightly from the geoid-undulation, due to problems in the exact definition of the center-of-gravity of the earth; the mass of the earth and the potential of the ellipsoid; and height differences between the reference surfaces (telluroid, elipsoid, geoid) and global topography. First, we apply the "zero-order undulation" correction, estimated at -53 cm for WGS'84 (subtract 53 cm from height-anomaly to obtain geoid-undulation). Second, we compute the effect of the height differences. This correction which was computed from EGM'96 harmonic coefficients came out insignificantly small (a few mm only). The third (and last) was a correction for the indirect-effect of topography potential, computed by Grushinski's formula. It also came out rather moderate in size (in the 0-2 cm range).

We summarize this section by listing the algorithm for predicting geoid undulations within the borders of our pilot project area. There are two distinct sequences:

Sequence a. Preparation of an undulation correction grid (or contour map) based on a selected sub-network of anchor points. Sequence (a) consists of the following steps:

• a-1 at each anchor point evaluate the height anomaly using a global gravity model.

• a-2 at each anchor point perform Stokes integration of residual f.a. anomalies.

• a-3 for each anchor point evaluate corrections for height anomalies / undulations.

• a-4 sum a-1, a-2 and a-3 and subtract the directly measured geoid undulation at the respective anchor points in order to create an undulation correction field.

• a-5 interpolate a-4 into a regular grid or a contour map.

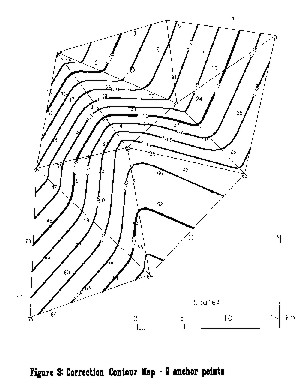
Figures 2 and 3 show two such correction contour maps prepared for two different anchor point bases, where Stokes integration (step a-2) was carried out up to an outer- limit of 2.0 degrees.

Sequence b. Prediction of geoid undulation at a given position. Computational steps:

• b-1 for the prediction point (f,l) evaluate and sum a-1, a-2 and a-3.

• b-2 interpolate a correction for (f,l) using the a-5 grid (or contour map).

• b-3 subtract b-2 from b-1 to obtain a prediction of the geoid undulation at (f,l).

Following the completion of the two leveling campaigns and the subsequent analysis and adjustment of the measurements we faced two problems regarding gravity data:

1. It was not clear how much the lack of consistent and reliable gravity data beyond the state's boundaries would affect the ultimate accuracy of undulation prediction. The gravity anomalies field at our disposal allowed Stokes integration only up to a distance (outer-limit) of 0.5^o.

2. Up to 1997 the only gravity model at our disposal was the OSU'91 model. The OSU model was developed without the benefit of directly measured gravity data from our region. We were not sure how much the above inherent deficiency of the model is going to affect our R&R process and consequently - our geoid undulation predictions.

Experiments with the new EGM'96 model in early 1998 brought a slight improvement to our predictions although we were still confined to the 0.5^o outer-limit for Stokes integration /Sharni et.al., 1998/. In order to meet our target accuracy of 4 cm (one-sigma) for an undulation difference within the project area we still had to keep distances between the anchor points too short for comfort (10 km in flat terrain and no more than 6 km in the mountain). By mid 1998, equipped with the brand new GPM'98B gravity model, we noted a much better fit to our directly measured undulations. Our efforts to extend the limits of Stokes integration up to 2.0^o were at last (early 1999) crowned with success. We were finally ready to perform a complete set of experiments and analyses.

We repeated Stokes integration (residual anomalies) for a succession of outer-limits, beginning with 0.5^oand up to a maximum of 2.0^o. The undulation correction field was interpolated on the basis of 28 anchor points (distances of 8-12 km in flat areas and 5-7 km in the mountain). Another set of interpolations was based on only 9 anchor points, the distances being now 13-17 km over the project area (see Figures 2 and 3).

Differences between predicted (b-3) and directly measured undulations at the check points were used by us to estimate the effective accuracy of the whole prediction process (See Table 1). As check points we denoted all those control points which did not serve as anchor points in preparing the undulation correction field (a-4). Note that in spite of containing much less detail (See Figure 3), the 9 anchor points correction contour map produced predictions of remarkably high accuracy. We went as far as to prepare a correction field based on only 5 anchor points (not shown in this paper). The resulting accuracy of prediction went down to 3 cm (one-sigma).

Table 1: Analysis of undulation prediction accuracy (66 control points).

In Table 1 we summarize results of our analyses for two outer-limits of integration. The remaining limits (0.8, 1.2 and 1.6 degrees) did not produce significantly different results so we left them out. The pleasant surprise was that we were nicely below the 2 cm one-sigma level with our predictions. The above table brought answers to both of our questions: (a) the best fitting properties of the global gravity model are indeed crucial for deriving a precise geoid in a given area; (b) the contribution of gravity anomalies beyond 0.5^o (50-60 km) can be defined at best as marginal.

This page is maintained by the FIG Office. Last revised on 15-09-04.